辗转相除法，又名欧几里德算法（Euclidean algorithm），是求两个正整数最大公约数的算法。它是已知最古老的算法之一，其可追溯至3000年前。用辗转相除法来得一个分数的约分后的最简形式的算法如下：

第一步：设两数为a、b，且令a>b；
第二步：a÷b，令r为所得余数，若r=0，算法结束，b 即为最大公约数；若r>0则a←b，b←r，并返回第二步；
第三步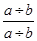：即为约分后的最简形式。
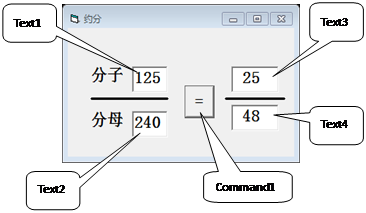
编写VB程序，程序运行界面如第6题图1所示，请根据算法将下列程序补充完整。
Private Sub Command1_Click()
Dim a As Integer, b As Integer, r As Integer 'a、b为分子和分母，r为最大公约数
a = Val(Text1.Text)
b = Val(Text2.Text)
If b =" 0" Then c = MsgBox("分母不能为0"): Exit Sub
'如果分母为0，则提示“分母不能为0”并退出该过程
r =         ①      
Text3.Text =" Str(a" / r)
Text4.Text =" Str(b" / r)
End Sub
Function gys(ByVal m As Integer, ByVal n As Integer) As Integer
'gys函数用于求最大公约数
Dim s As Integer
If m < n Then
t =" m:" m =" n:" n = t
End If
Do While n <> 0
s =" m" Mod n
m = n
n = s
Loop
       ②     
End Function